Konsep Distribusi Sampel dan Uji Hipotesa dalam Statistika
Konsep Distribusi Sampel dan Uji Hipotesa dalam Statistika - Hipotesa didefiniskan sebagai pernyataan yang bersifat dugaan mengenai adanya hubungan antara 2 variabel atau lebih. Pernyataan mengenai dugaan hubungan antara dua variabel tersebut sifatnya masih lemah kebenarannya, sehingga masih perlu dibuktikan dengan menggunakan perhitungan statistika.
Hipotesa yang sudah dapat dibuktikan kebenarannya akan disebut sebagai tesa. Dua variabel yang akan dibuktikan dibedankan menjadi independent variable (IV) dan dependent variable (DV). Independent variable (IV) adalah variabel yang dihipotesakan mempengaruhi dependent variable (DV). Sebagai contoh suatu penelitian memiliki hipotesa intelegensi (IQ) yang dimiliki anak desa akan berbeda dengan intelegensi yang dimiliki oleh anak kota. Maka dapat dinyatakan:
Hipotesa : ada perbedaan IQ antara anak desa dan kota
Variabel I (DV): nilai IQ
Variabel II (IV): tempat tinggal yang bervariasi
Tujuan Pengujian Hipotesa
Tujuan pengujian hipotesa bukan dimaksudkan untuk membuktikan apakah hipotesa benar atau salah, tetapi bertujuan untuk mengumpulkan kenyataan-kenyataan yang mendukung atau tidak mendukung hipotesa. Dalam penguhian hipotesa yang dilihat adalah seberapa besar kemungkinan hipotesa dapat dibuktikan atau tidak. Dalam statistika pengujian hipotesa akan memiliki kemungkinan untuk memperoleh hasil 95% atau 99% hasil yang mendekati kenyataannya, namun dalam pengujian hipotesa tidak mungkin untuk mendapatkan hasil yang 100% sama dengan kenyataan.
Macam-macam Hipotesa Penelitian
Ada beberapa macam hipotesa, di antaranya:
Hipotesa Nol dan Hipotesa Alternatif
Hipotesa Nol (H0) menyatakan tidak ada hubungan antara variabel-variabel yang diteliti, atau perbedaan antara dua kelompok yang ditemukan dengan penelitian hanya disebabkan faktor kebetulan. Sementara hipotesa alternatif (H1) menyatakan bahwa ada hubungan antara variabel-variabel yang diteliti, dan perbedaan yang ditemukan pada dua kelompok yang diteliti bukan disebabkan oleh kebetulan.
Dalam penelitian akan berusaha untuk menolak H0, maksudnya adalah penelitian ditujukan untuk membuktikan pernyataan bahwa tidak ada perbedaan antara variabel-variabel yang diteliti itu tidak benar. Jika H0 berhasil ditolak, maka H1 diterima, yang maksudnya adalah terdapat perbedaan antara dua variabel yang diteliti, dan perbedaan tersebut bukan disebabkan oleh kebetulan.
Dalam pengujian hipotesa terdapat dua macam pengujian jika dilihat dari arah pengujiannya, yaitu: Pengujian 2 arah (two-tail test) dan Pengujian 1 arah (one-tail test)
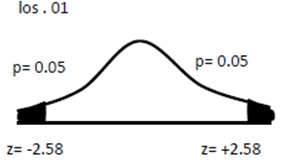
1. Pengujian 2 arah (two-tail test)
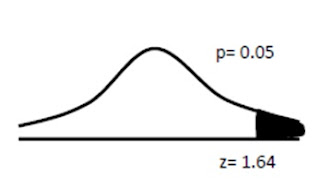
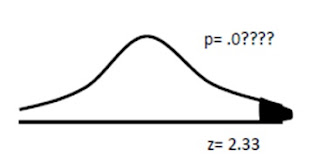
2. Pengujian 1 arah (one-tail test)
Critical region
Critical region afalah daerah untuk menolak Ho, atau daerah untuk kejadian-kejadian yang mempunyai probabilitas untuk timbul sangat kecil, yang berada di bawah H0 (p ≤ 0.01).
Jadi dalam kejadian yang probabilitasnya sangat kecil memang terjadi memang betul2 ada perbedaan antara kedua Mean kelompok, bukan karena fakta kebetulan.
Matriks Pengambilan Keputusan
Hipotesa yang sudah dapat dibuktikan kebenarannya akan disebut sebagai tesa. Dua variabel yang akan dibuktikan dibedankan menjadi independent variable (IV) dan dependent variable (DV). Independent variable (IV) adalah variabel yang dihipotesakan mempengaruhi dependent variable (DV). Sebagai contoh suatu penelitian memiliki hipotesa intelegensi (IQ) yang dimiliki anak desa akan berbeda dengan intelegensi yang dimiliki oleh anak kota. Maka dapat dinyatakan:
Hipotesa : ada perbedaan IQ antara anak desa dan kota
Variabel I (DV): nilai IQ
Variabel II (IV): tempat tinggal yang bervariasi

|
| image source: |
baca juga: Konsep dan Contoh Soal Distribusi Normal dan Z Score
Tujuan Pengujian Hipotesa
Tujuan pengujian hipotesa bukan dimaksudkan untuk membuktikan apakah hipotesa benar atau salah, tetapi bertujuan untuk mengumpulkan kenyataan-kenyataan yang mendukung atau tidak mendukung hipotesa. Dalam penguhian hipotesa yang dilihat adalah seberapa besar kemungkinan hipotesa dapat dibuktikan atau tidak. Dalam statistika pengujian hipotesa akan memiliki kemungkinan untuk memperoleh hasil 95% atau 99% hasil yang mendekati kenyataannya, namun dalam pengujian hipotesa tidak mungkin untuk mendapatkan hasil yang 100% sama dengan kenyataan.
Macam-macam Hipotesa Penelitian
Ada beberapa macam hipotesa, di antaranya:
- Hipotesa Konseptual, yaitu hipotesa yang menyatakan hubungan antara dua variabel atau lebih. Misal: taraf kecerdasan anak-anak kota lebih baik daripada anak-anak desa.
- Hipotesa Operasional, merupakan hipotesa masih harus dioperasionalisasikan sebelum dapat diuji.
- Hipotesa Statistik, yaitu pernyataan yang menyatakan hubungan antara dua variabel dengan menggunakan istilah-istilah statistik dan kuantitatif. Misal: rata-rata skor tes anak kota lebih tinggi daripada rata-rata skor anak desa:
Hipotesa Nol (H0) menyatakan tidak ada hubungan antara variabel-variabel yang diteliti, atau perbedaan antara dua kelompok yang ditemukan dengan penelitian hanya disebabkan faktor kebetulan. Sementara hipotesa alternatif (H1) menyatakan bahwa ada hubungan antara variabel-variabel yang diteliti, dan perbedaan yang ditemukan pada dua kelompok yang diteliti bukan disebabkan oleh kebetulan.
Dalam penelitian akan berusaha untuk menolak H0, maksudnya adalah penelitian ditujukan untuk membuktikan pernyataan bahwa tidak ada perbedaan antara variabel-variabel yang diteliti itu tidak benar. Jika H0 berhasil ditolak, maka H1 diterima, yang maksudnya adalah terdapat perbedaan antara dua variabel yang diteliti, dan perbedaan tersebut bukan disebabkan oleh kebetulan.
Dalam pengujian hipotesa terdapat dua macam pengujian jika dilihat dari arah pengujiannya, yaitu: Pengujian 2 arah (two-tail test) dan Pengujian 1 arah (one-tail test)
1. Pengujian 2 arah (two-tail test)
Critical region afalah daerah untuk menolak Ho, atau daerah untuk kejadian-kejadian yang mempunyai probabilitas untuk timbul sangat kecil, yang berada di bawah H0 (p ≤ 0.01).
Jadi dalam kejadian yang probabilitasnya sangat kecil memang terjadi memang betul2 ada perbedaan antara kedua Mean kelompok, bukan karena fakta kebetulan.
Matriks Pengambilan Keputusan
Ketika seorang peneliti melakukan analisa dan pengambilan keputusan, ada dua kemungkinan kesalahan yang dapat dilakukannya. Kedua kesaahan itu antara lain kesalahan tipe I dan kesalahan tipe II.
Kesalahan Tipe I (α) terjadi ketika kita menolak Ho, padahal Ho benar. Pada kesalahan Tipe I peneliti memutuskan ada perbedaan pada variabel-cariabel yang diteliti, padahal tidak ada perbedaan antara variabel-variabel; yang diteliti tersebut. Pada penelitian, perbedaan yang terjadi antara variabel-variabel disebabkan okeh kebetulan.
Kesalahan Tipe II (β) terjadi ketika peneliti memutuskan bahwa H0 gagal ditolak, padahal seharusnya H0 seharusnya ditolak. Peneliti melakukan kesalahan karena menganggap tidak ada perbedaan antara variabel-variabel yang diteliti, padahal sebenarnya terdapat perbedaan antara variabel-variabel yang diteliti.
Probabilitas Kesalahan Tipe I dan Tipe II
Probabilitas peneliti membuat kesalahan dalam menganalisa hasil yang didapat dari pengujian dipengaruhi oleh α (alpha) atau tingkat probablitas peneliti untuk menolak H0. Jika peneliti menggunakan standard α yang besar, maka semakin besar probabilitas kesalahan yang mungkin terjadi. Sementara, semakin kecil standard nilai α yang digunakan, maka semakin kecil pula probabilitas peneliti melakukan kesalahan Tipe I.
Misal:
Nilai α = .05, diartikan bahwa terdapat probabilitas 5 dari 100 peneliti salah dalam menolak H0, padahal Ho benar. Pada α = .01, terdapat probabilitas 1 dari 100 peneliti melakukan kesalahan dalam menolak H0. Hal tersebut jelas menunjukkan Makin kecil nilai α, makin kecil pula kemungkinan kesalahan tipe I.
Mengapa tidak membuat α sekecil mungkin? Karena jika kesalahan Tipe I (α) diperkecil, maka kesalahan tipe II justru naik, sehingga kemungkinan peneliti gagal menolak H0 padahal Ho salah menjadi lebih besar.
Catatan:
LATIHAN
Sekian artikel tentang Konsep Distribusi Sampel dan Uji Hipotesa dalam Statistika. Semoga bermanfaat.
Daftar Pustaka
Kesalahan Tipe I (α) terjadi ketika kita menolak Ho, padahal Ho benar. Pada kesalahan Tipe I peneliti memutuskan ada perbedaan pada variabel-cariabel yang diteliti, padahal tidak ada perbedaan antara variabel-variabel; yang diteliti tersebut. Pada penelitian, perbedaan yang terjadi antara variabel-variabel disebabkan okeh kebetulan.
Kesalahan Tipe II (β) terjadi ketika peneliti memutuskan bahwa H0 gagal ditolak, padahal seharusnya H0 seharusnya ditolak. Peneliti melakukan kesalahan karena menganggap tidak ada perbedaan antara variabel-variabel yang diteliti, padahal sebenarnya terdapat perbedaan antara variabel-variabel yang diteliti.
Probabilitas Kesalahan Tipe I dan Tipe II
Probabilitas peneliti membuat kesalahan dalam menganalisa hasil yang didapat dari pengujian dipengaruhi oleh α (alpha) atau tingkat probablitas peneliti untuk menolak H0. Jika peneliti menggunakan standard α yang besar, maka semakin besar probabilitas kesalahan yang mungkin terjadi. Sementara, semakin kecil standard nilai α yang digunakan, maka semakin kecil pula probabilitas peneliti melakukan kesalahan Tipe I.
Misal:
Nilai α = .05, diartikan bahwa terdapat probabilitas 5 dari 100 peneliti salah dalam menolak H0, padahal Ho benar. Pada α = .01, terdapat probabilitas 1 dari 100 peneliti melakukan kesalahan dalam menolak H0. Hal tersebut jelas menunjukkan Makin kecil nilai α, makin kecil pula kemungkinan kesalahan tipe I.
Mengapa tidak membuat α sekecil mungkin? Karena jika kesalahan Tipe I (α) diperkecil, maka kesalahan tipe II justru naik, sehingga kemungkinan peneliti gagal menolak H0 padahal Ho salah menjadi lebih besar.
Catatan:
- Besarnya αdan β ditentukan oleh peneliti
- Hubungan α dan β terbalik
LATIHAN
- Apa itu hipotesa dan fungsi dari hipotesa dalam penelitian. Jelaskan
- Sebutkan tipe-tipe hipotesa. Jelaskan
- Apa beda one-tailed test d engan two-tailed test?
- Jelaskan perbedaan error tipe I dan error tipe II
Sekian artikel tentang Konsep Distribusi Sampel dan Uji Hipotesa dalam Statistika. Semoga bermanfaat.
Daftar Pustaka
- Aron, A., Coups, E.J., & Aron, E.N. (2013). Statistics for psychology. 6th ed. New Jersey: Pearson Education, Inc.
- Gravetter, F.J. & Wallnau, L.B. (2009). Statistics for the Behavioral Sciences.
- Hinton, P.R. (2004). Statistics Explained, 2nd ed. London: Routledge.
- Howell, D.C. (2012). Statistical Method for Psychology. Australia: Wadsworth, Cengage Learning.
- Nolan, S.A. & Heinzen, T.E, (2012). Statistics for the Behavioral Sciences. Second Edition. New York: Worth Publishers.
- Sulistiyono, S. (2009). Statistika Psikologi 2. Jakarta: Fakultas Psikologi Universitas Mercu Buana.





Posting Komentar untuk "Konsep Distribusi Sampel dan Uji Hipotesa dalam Statistika"